Ni lotería de Navidad ni Euromillones

Ni lotería de Navidad ni Euromillones, este es el sorteo con el que es más fácil hacerte millonario.

Según el regulador del juego (la DGOJ) en 2023 los operadores de juego recibieron apuestas por valor de 48.000 millones y después de pagar premios ganaron 7.300 millones (0,5 % del PIB). Esto quiere decir que, si eres un adulto en la media, el año pasado hiciste apuestas en juegos de azar por valor de 1.250 € y terminaste perdiendo 190 €. Y de esos 190 € casi 130 € los perdiste en loterías.

A lo largo de su vida el adulto medio jugará más de 21.000 € solo en loterías, de los que perderá más de 8.000 €. La única razón por la que esto no nos parece raro es porque nos han comido la cabeza, como tan bien explicó Lord Draugr en un vídeo muy popular que publicó el año pasado.

La lotería es un juego que se vende con retórica de «país de piruleta», ilusión, tradición y comunidad, pero que, igual que los bancos centrales, tiene un origen violento. El primer sorteo público de loterías que se ha documentado ocurrió en Milán en enero de 1449 para financiar las campañas militares de la ciudad contra Venecia. En España la lotería moderna nació en Cádiz en 1811, por iniciativa de Ciriaco González Carvajal, para financiar la Guerra de la Independencia.

¿Y por qué destinamos esas cantidades al juego? ¿Acaso no sabemos que vamos a perder?

El concepto clave aquí es la esperanza matemática o valor esperado. Para calcular el valor esperado de una apuesta hay que sumar los premios potenciales multiplicados cada uno por su probabilidad. Si el resultado es menor que el coste de jugar perderás dinero a largo plazo. Y ese es precisamente el otro punto subordinado, el largo plazo. Incluso aunque el valor esperado (una vez descontado el coste de jugar) sea positivo y vayas a ganar dinero, quizá ese largo plazo sea demasiado largo (aquí podemos hablar de la varianza o de la dispersión de los premios). Por ejemplo, puedes apostar a un juego en el que ganes 10 € con una probabilidad del 10 % o a otro en el que ganes 100 € con una probabilidad del 1 %. En ambos casos el valor esperado es 1 € y si el coste de jugar es inferior, pongamos de 0,5 €, terminarás ganando el mismo dinero a largo plazo. Pero en el corto plazo podrías experimentar pérdidas, y estas serán más grandes, duraderas y probables en el segundo juego que en el primero.

No obstante, el valor esperado no es del juego, sino de la estrategia concreta. Hay juegos en los que todas las estrategias posibles tienen el mismo valor esperado, por ejemplo, la lotería de Navidad: da igual cómo elijas el número, la probabilidad de resultar premiado es la misma. Pero hay otros en los que la estrategia puede ser determinante.

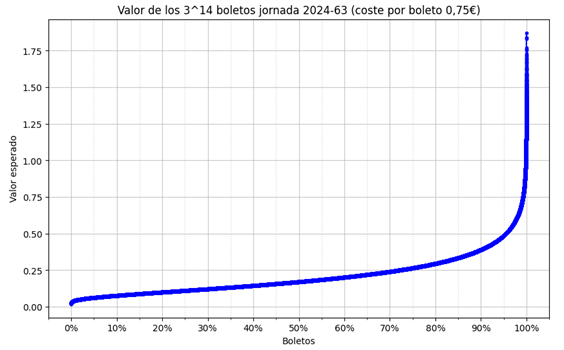
Por ejemplo, la quiniela es en general un juego malísimo, ya que solo reparte en premios el 55 % de lo recaudado. Es decir, el valor esperado jugando un boleto al azar o el valor esperado del jugador medio es de 0,55 € por euro jugado. Sin embargo, ya que resultar premiado depende de ciertos eventos deportivos (cuya probabilidad se puede calcular) y el importe de esos premios depende del número de acertantes (que también se puede calcular con los datos de boletos sellados que publica diariamente Loterías y Apuestas del Estado) es posible encontrar boletos con valores esperados positivos.

Otro ejemplo podrían ser las apuestas deportivas. Solo considerando que hay unos pocos jugadores con cierta habilidad para ganar de forma sistemática a las casas de apuestas podemos explicar la distribución de resultados por percentiles. En el póquer ocurre lo mismo. Incluso en la ruleta tenemos ejemplos históricos de estrategias exitosas como los famosos Pelayos, que medían estadísticamente imperfecciones o los Eudaemonics con su predicción balística. En cualquier caso, esto son anomalías que solo con habilidad y suerte pueden llegar a explotarse. Lógicamente, para que cualquier juego de azar sobreviva en el tiempo debe ser rentable para el que lo organiza. Esto implica que los jugadores, en agregado, deben palmar pasta. Puede haber ganadores sistemáticos, pero que sean poquitos, o pueden ser muchos pero durante poco tiempo hasta que la estrategia deje de ser explotable o el organizador quiebre.

Entonces, ¿por qué participamos en juegos de azar? Se me ocurren tres posibles razones:

Hemos encontrado una estrategia con valor esperado positivo (o creemos haberla encontrado). No creo que sea el caso de la mayoría, pero sí de muchos más de los que la gente cree. Primero, porque hay muchos apostadores ganando de forma sistemática con estrategias variadas (principalmente en el segmento de apuestas deportivas y póquer). Y segundo, porque hay muchos más que juegan porque creen que terminarán ganando y en realidad se equivocan.

Nuestra estrategia tiene valor esperado positivo cuando ajustamos con valoraciones subjetivas. Me refiero a que no todos los euros valen lo mismo. Si te toca un premio de 1 millón te alegras mucho, si te tocan 2 millones no te alegras el doble. Si te toca un millón con 20 años mola, si te toca con 70 años mola, pero menos. Gastarte 15 € al mes en loterías o no gastarlos puede no cambiarte la vida un ápice. Conseguir medio millón antes de los 50, sí. Bueno, puede ser una justificación razonable. Por eso no me gusta el Euromillones, por ejemplo. El premio mínimo son 15 millones. ¿Para qué narices quiero 15 millones? Dame uno y medio con una probabilidad 10 veces superior y a lo mejor compro. Con millón y medio y cuatro nociones de finanzas tienes la vida resuelta. Hay pocas cosas que no te puedas permitir con 1,5 M y sí con 15 M.

Nuestra estrategia es perdedora pero la valoración subjetiva de la ilusión que nos genera el juego lo compensa. Es decir, estamos comprando ilusión o cualquier otra mierda del estilo, como la envidia, tradición o el sentirse parte de un grupo. «Es que en mi trabajo todos compran, mira que como les toque y yo no haya comprado…».

Probablemente esta última es la razón por la que la mayoría juega ciertos sorteos, por envidia preventiva. Te recuerdo que no es obligatorio comprar lotería. Si a tus compañeros de trabajo, familiares, amigos o vecinos les toca, pues genial; ascenderás, heredarás, te invitarán a algo o les venderás cosas. De hecho, si asumes que no vas a jugar, mejor que les toque a ellos antes que a alguien random.

Me queda un último punto que tratar: el riesgo. ¿Por qué es tan generalizado y popular exponerse a la incertidumbre de esta forma tan artificial? Tengo una teoría: es un epifenómeno, una consecuencia secundaria derivada del déficit de incertidumbre crónico en las sociedades modernas.

Vivimos en un mundo en el que el Estado nos garantiza un sueldo fijo, nos garantiza una pensión, nos garantiza salud, nos garantiza que lo que compramos ha pasado controles de calidad, si nos quedamos sin empleo, si hay una catástrofe natural… No sabemos gestionar la incertidumbre porque jamás nos hemos enfrentado a ella. El Estado la mató. Pero asumir cierto nivel de incertidumbre fue (y es) probablemente una conducta exitosa a lo largo de nuestra trayectoria evolutiva. Nuestra naturaleza nos impulsa a ello. Quizá en las sociedades modernas hayamos encontrado en el juego un sustituto artificial para «masturbar» este deseo.

Pero, sea como sea, tú has hecho clic en este artículo porque quieres 1 millón de euros de forma fácil y rápida, así que vamos a ello.

Aquí es donde deberíamos ponernos a calcular la esperanza matemática de todos estos juegos para decidir a cuál jugar. Pero hay una forma más sencilla que liarnos con sesudos cálculos: ir a mirar los márgenes agregados.

Según los datos de 2023 comunicados por los operadores a la DGOJ vemos que el segmento loterías gana casi un 40 % de lo jugado. Es decir, a largo plazo por cada euro jugado cobrarás en premios 0,6 €. En cambio, los segmentos «Casino» y «Apuestas» tienen menor margen para la casa y mayor por tanto para el jugador.

Así que, puestos a tirar el dinero en lotería, permíteme ofrecerte tres alternativas más baratas:

Con los 20 € que te dejas en la lotería de Navidad, te vas a la ruleta. Busca una que tenga un límite máximo elevado. Eliges un número y lo apuestas todo. Si aciertas, vuelves a elegir y a apostar todo de nuevo. Y luego, otra vez. Solo tienes que acertar 3 veces seguidas y saldrás de ahí con 933.120 €. Y la probabilidad de que esto ocurra es de 1 entre «solo» 50.653. Vale, es difícil, pero ¿y si toca?

Hazte una combinada en alguna casa de apuestas online. Busca cuatro pronósticos que estén a cuota 15 y apuestas de forma combinada de tal forma que solo cobres si aciertas los 4. Si apuestas los 20 €, cobrarás 1.012.500 €. Y esto ocurrirá aproximadamente 1 de cada 54.675 veces, mucho más probable que la lotería de Navidad.

Busca un bróker online que permita apalancarse 1 a 2.500. No es frecuente, pero alguno hay cumpliendo condiciones. El 1 de enero metes los 200 € que te ibas a dejar ese año en gaming, lo apalancas para que se conviertan en 500.000 € y lo inviertes todo en una empresa random del S&P 500. Cada año hay 2 o 3 empresas que se multiplican por 3, así que, con un poco de suerte (y cruzando dedos para comprar en mínimos del año) tendrás una probabilidad de 3 entre 500 de terminar el año con 1 M de beneficios.

Cualquiera de estas opciones mejora el resultado de la lotería de Navidad. Pero igual, solo igual, hay mejores formas de emplear el fruto de tu esfuerzo…

P.D.: Y si te toca, ¿qué haces? Pues esto no.

Referencias:

https://cejuego.com/

https://www.ordenacionjuego.es/es/datos-mercado-espanol-juego

https://www.ine.es/jaxiT3/Tabla.htm?t=24884&L=0

https://www.youtube.com/watch?v=2JbekXAtveg

https://www.slickcharts.com/sp500/performance

https://x.com/inga1937/status/1639533623589126144

https://x.com/papa2fire/status/1341308142739722240

https://x.com/papa2fire/status/1606246258271784961

https://x.com/papa2fire/status/1605858200359682050

https://x.com/papa2fire/status/1423720535486353408