Cuando nos decidimos a invertir en productos financieros como forma de hacer crecer nuestros ahorros e intentar que no desaparezcan por culpa de la inflación, siempre es recomendable que nos lo planteemos a largo plazo, y ello por dos motivos. El primero, por la propia volatilidad de los mercados de renta variable. Al invertir a plazos largos, la volatilidad queda amortiguada y no estaremos al albur del caprichoso comportamiento en el corto plazo.

Aunque no hay una regla, un plazo de siete años se considera aceptable por la mayor parte de gestores profesionales; lo tomaremos como referencia, de modo que siete años será el plazo mínimo para invertir en renta variable. Si estimo que necesitaré antes ese dinero, asumiré que no lo podré invertir en renta variable y deberé tenerlo en opciones más líquidas para que no sean tan volátiles.

El segundo motivo es porque ahorrar pequeñas cantidades muy pronto puede ser tan efectivo como ahorrar mayores cantidades más tarde. En este artículo me centraré en esta idea y veremos que es conveniente pensar en objetivos lejanos (ejemplo, la universidad de un hijo, aunque sea un bebé; o la posibilidad de comprar una casa, aunque ahora siendo joven no lo consideres posible ni viable económicamente) e ir asignando ahorro a esos objetivos, aunque sea con cantidades modestas. Como es contraintuitivo que con poco dinero y mucho tiempo por delante se puedan alcanzar los mismos objetivos que con mucho más dinero, lo veremos con un ejemplo.

Alberto y José son dos gemelos y ganan lo mismo: 2.000 euros netos al mes, es decir, 24.000 euros anuales después de pagar la Seguridad Social y sus impuestos de la renta. Los dos quieren ahorrar con la idea de comprarse cada uno un piso dentro de quince años. A esas «bolsas de ahorro» las llamaremos «mochila-casa», porque ese es su objetivo: llenar la mochila de euros con los que pagar la entrada (¡y los impuestos de compra!) de su piso. Eso sí, cada uno ahorrará a su manera.

Alberto prefiere apretarse ahora el cinturón y ahorrar 400 euros al mes durante tres años. Así, ahorrará 14.400 € (400 € x 12 meses x 3 años).

José prefiere ahorrar siempre lo mismo, así que ahorrará 80 euros al mes durante cada uno de los quince años. Son también 14.400 € (80 € x 12 meses x 15 años).

Como saben de la volatilidad de los mercados, no invertirán a menos de 7 años, así que lo que ahorren después del octavo año (años nueve a quince) ya no podrán invertirlo, porque les quedarán menos de siete años hasta llegar a los quince años de plazo total que se han dado para comprarse el piso. Así que Alberto podrá invertir todos los ahorros porque ha ahorrado los primeros tres años, y luego tendrá doce años por delante sin tener que ahorrar nada más; y José, lo que ahorre después del octavo año, no lo invertirá.

Ambos lo invierten en el mismo fondo indexado global, cuyo rendimiento histórico es del 7 %, porque es un fondo vinculado al índice MSCI World y consigue replicarlo casi a la perfección (el MSCI World tuvo una rentabilidad media histórica del 7,9 % los últimos 20 años, y si bien los fondos tienen un tracking error, es razonable asumir un 7 % de rentabilidad futura probable). Recuerda que los fondos indexados globales no rinden un constante 7 % cada año porque son volátiles. Rendirán unos años más y otros menos o perderán dinero, pero la media histórica es del entorno del 7 %, valor con el que se realizan los cálculos; y en periodos largos, esta simplificación es correcta. Que rindan más o menos no afecta a la explicación de por qué los plazos de inversión importan: cambiarán las cantidades totales ahorradas, pero no la «proporción» entre lo que alcancen Alberto y José.

Así que cada año Alberto y José ahorrarán:

 

 

 

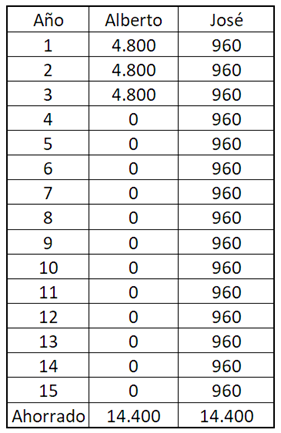
¿Cómo será la «mochila-casa» de Alberto?

Al final del primer año (recuerda que sería mensualmente, pero he realizado la tabla anualmente para simplificar el ejemplo) ha ahorrado 4.800 euros. Así que este primer año los 4.800 euros solo le vienen del ahorro.

En el segundo año invertirá esos 4.800 euros del primer año, que deberían revalorizarse (plusvalía) en 336 euros (4.800 x 7 %), para un total de 5.136 euros (4.800 + 336); y a ello se le sumarán los 4.800 euros ahorrados durante el segundo año, por lo que tendrá al final de año unos 9.936 euros (5.136 + 4.800).

Durante el tercer año ahorrará 4.800 euros, que se sumarán a lo que se revaloricen los previos 9.936 euros invertidos, unos 696 euros (9.936 x 7 %), total de 15.432 euros (4.800 + 9.936 + 696).

A partir del cuarto año ya no ahorrará nada, y lo que tenga al final de ese año vendrá de lo que crezca lo que acumula su inversión en el año pasado (15.432 euros), y que debería crecer en unos 1.080 euros (15.432 x 7 %), total de 16.512 euros (15.432 +1.080); y así los años sucesivos, porque, como desde que lo ahorró (en los años uno, dos y tres) hasta que acaben los quince años hay más de siete años de horizonte de inversión, lo mantiene invertido hasta el final. Al final de los quince años tendrá unos 34.756 euros.

Lo tienes resumido en la tabla siguiente:

 

 

 

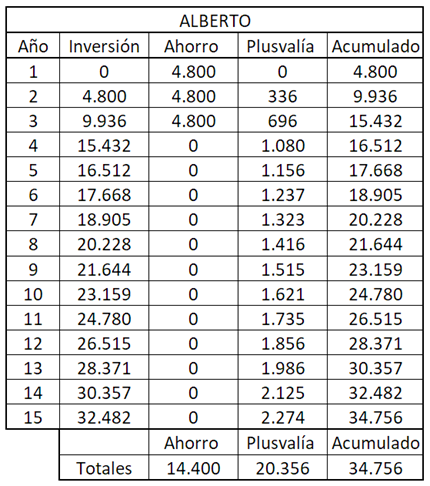
¿Y qué pasaría en el caso de la mochila-casa de José?

José en los primeros tres años sería como su hermano, aunque ahorrando anualmente 960 euros en vez de 4.800 euros. Y al final de año, los invierte.

El primer año tendrá 960 euros fruto de su ahorro, que invertirá a partir del segundo año. En el segundo año invertirá esos 960 euros ahorrados el primer año, inversión que debería revalorizarse (plusvalía) en 67 euros (960 x 7 %), para un total de 1.027 euros (960 + 67); y a ello se le sumarán los 960 euros ahorrados en el segundo año, por lo que tendrá al final de año unos 1.987 euros (960 + 960 + 67).

Durante el tercer año ahorrará 960 euros que se sumarán a los 139 euros que se hayan revalorizado los previos 1.987 euros (1.987 x 7 % = 139 euros total de 3.086 euros (1.987 + 960 + 139), y así hasta acabar… el octavo año. ¿Por qué?

Porque el noveno año ya estaría a menos de siete años para acabarse el plazo de quince años que se dio para pagar la entrada de su «mochila-casa», y por ser inferior a siete años el horizonte de inversión no deberá invertirlo para que la volatilidad del fondo indexado global no le juegue una mala pasada. Seguirá ahorrando anualmente 960 euros, pero no los invertirá a final de año. Eso sí, lo ahorrado e invertido en los primeros ocho años seguirá invertido porque se «generaron» con un horizonte de más de siete años. Su ahorro e inversión hasta el octavo año quedará así:

 

 

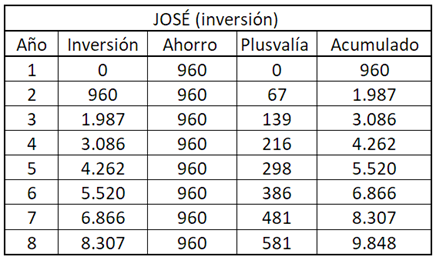
A partir del noveno año seguirá con su «mochila-casa», donde seguirá invertido lo acumulado hasta el octavo año (9.848 euros) hasta acabar los quince años totales; pero los 960 euros que ahorre en ese año ya no los invertirá e irán a una cuenta corriente.

La parte invertida durante ese noveno año generará una plusvalía de 689 euros (9.848 x 7 %), para un total acumulado en inversión de 10.537 euros (9.848 + 689); y así sucesivamente, esperando un aumento de un 7 % cada año. Quedaría así:

 

 

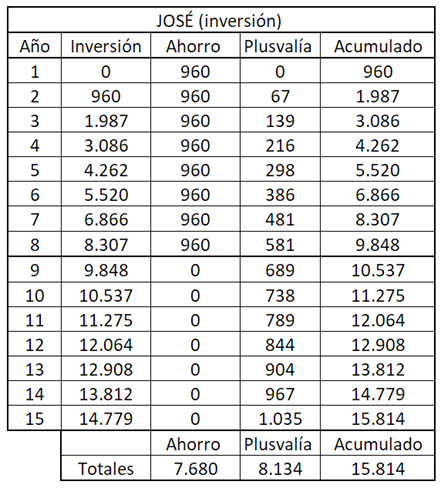
Los 960 euros del ahorro del noveno año estarán en una cuenta corriente y ya no generará plusvalías, por lo que se irán acumulando a razón de 960 euros durante siete años hasta un total de 6.720 euros al acabar el año quince.

 

 

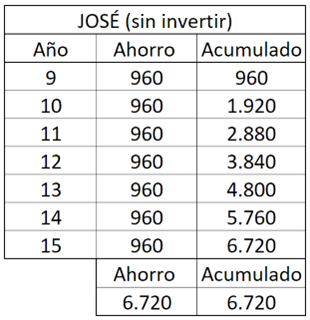
De este modo, en su dinero invertido espera tener 15.814 euros y en su parte no invertida 6.720 euros, total de 22.534 euros para la entrada del piso.

Por si lo quieres todo en una única tabla para comparar año a año con Alberto, te la dejo aquí:

 

 

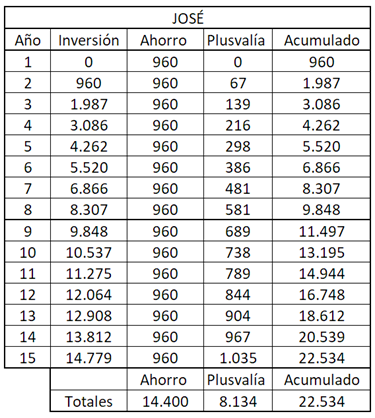
Como ves, habiendo invertido la misma cantidad de 14.440 euros, y en el mismo producto, la diferencia es de 12.222 euros, que representa un 54 % de diferencia. Estos 12.222 euros son «dinero gratis» que se lleva Alberto gracias al efecto del interés compuesto por haber tenido su inversión durante más tiempo.

Alberto eligió el ático, y José vivirá en el primero.

Esta ventaja de «ahorrar mucho pronto» en vez de «ahorrar poco tarde» puede ser también utilizada en aquellos casos de la compra de un piso en pareja, como veremos con el ejemplo de Rebeca y de Juan. Por simplificar, mantendremos el plazo de quince años de los gemelos en esta compra del piso.

Juan es más relajado y hará como hizo José. Ahorrará 960 euros anuales, y acumulará 22.534 euros. La tabla sería la misma que la indicada para José. Sin embargo, Rebeca prefiere hacer como Alberto y apretarse el cinturón los primeros tres años para luego olvidarse del asunto. Si ahorrara como José, acumularía unos 34.756 euros, y la idea es que ella aporte lo mismo que Juan.

Haciendo los cálculos en sentido inverso, a Rebeca le bastaría con ahorrar unos 3.112 euros anuales durante tres años, un total de 9.337 euros de ahorro para alcanzar la misma cifra que Juan. De modo que con unos 5.000 euros menos de ahorro, alcanzará los 22.534 euros de Juan, y podrá dedicar esos 5.000 euros a otros fines. Aquí tienes el detalle:

 

 

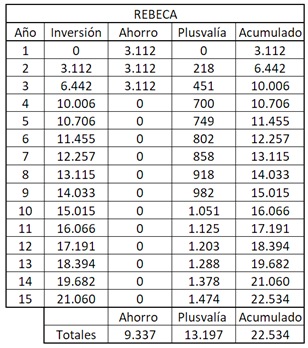
Como ves, empezar a ahorrar e invertir antes es igual de importante que la cantidad que ahorres e inviertas. Los que pudiendo ahorrar demoran la decisión, están perdiendo la posibilidad de acumular más dinero para sus proyectos o su jubilación. La buena noticia es para aquellos a los que les cuesta ahorrar; para ellos, empezar pronto con cantidades más pequeñas tendrá el mismo efecto que empezar más tarde con cantidades mayores.

 

Imagen generada con IA